CS267 Assignment 2

Optimizing Square Matrix Multiplication on the NOW

Compiling the assignment

There's no Makefile, sorry, however there's a compile script:

% source flabmul.build

Doing this will create flabmul, the benchmarking executable.

Optimizations used or attempted

Inner loop efficiency
The straightforward dot-product implementation produces code with a load-to-flop ratio of 2:2, and is therefore doomed to perform worse than half the maximum performance just because of the load bottleneck (the UltraSparc processor can only perform 1 load or store per cycle). Since the UltraSparc has many registers (32 double-floating-point registers), the solution was to compute 4 dot-products simultaneously from two rows of A and two columns of B. The load-to-flop ratio becomes acceptable at 4:8, as can be seen in the inner loop of MultiplyExB1xE and MultiplyExFxE.

Writing a good inner loop by hand was attempted but was not successful. Therefore we relied on the compiler to unroll the inner loops and schedule the instructions appropriately.

Extra compiler optimizations added

-xrestrict=%all, tells the compiler that no nasty aliasing is taking place.
-dalign, tells the compiler that every double is properly aligned.

Exploiting the caches
We compute the matrix multiplication in blocks of 128x128 to help locality. The actual value "128" was found by trial and error. For large matrices (n >= 96), it was found that spending some time copying the two blocks into a 128K contiguous array before proceeding with the multiplication was beneficial, most probably because otherwise the matrices A and B kick each other out of the L2 cache as they are accessed.

Specialized multiplication routines
The compiler does a better job of scheduling the inner loop when the loop bounds are known at compile time. Since most of the time the loop bound will be 128, we have a routine MultiplyExB1xE specialized for that loop size.

Handling odd-sized matrices
The routine MultiplyFxFxF is used to handle blocks with an odd number of row and columns. It is so inefficient that care was taken in the blocking strategy to create blocks of size either even or 1.

Results on the NOW

Our results are available in the file results-now-dgemm and are plotted below.

Since finding the right compile flags was part of the optimization process, the results are compared with basic_dgemm.c compiled using only the options suggested by the TA.

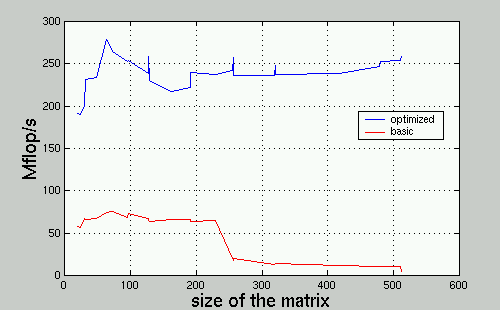
The little spikes up when the size is 128, 256 and 320 are caused by the highly efficient copying from memory to our local array when the data are well-aligned. Without copying, these sizes usually create spikes down on a performance graph because of cache conflicts.

Results on a Pentium II 300MHz

Both dgemm.c and basic_dgemm.c were compiled using gcc -O3.

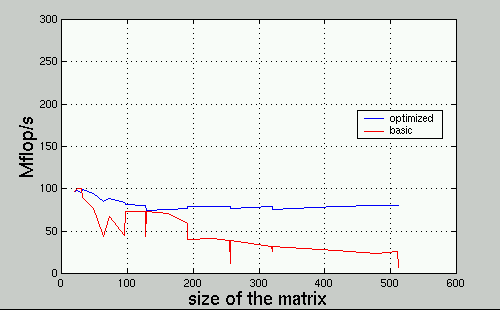
The blocking and copying techniques seem to help on this architecture as well, since the blue curve stays flat as the size of the matrix increase. However the simultaneous-4-dot-products technique doesn't seem to help at all, probably because the Pentium II processor is notorious for having a small set of (8?) floating-point registers.

Finally, we would like to thank Steve Chien for telling us about the -xrestrict=%all flag which helped us gain an extra 15-or-so Mflop/s.

François Labelle Ping (Peter) Jiang Jingang Yi