Detailed Description
Describes the generic, matrix type-independent kernel implementations called by the user.
This implementation includes five kernels:
- oski_MatMult: Sparse matrix-vector multiply.
- oski_MatTrisolve: Sparse triangular solve.
- oski_MatTransMatMult: Sparse
 .
. - oski_MatMultAndMatTransMult: Simultaneous computation of
 and
and  .
. - oski_MatPowMult: Sparse matrix powers times a vector, i.e.,
 .
.
The basic outline of each kernel's implementation is the same. Let the kernel call be KERNEL( A_tunable, ... ) where A_tunable is the matrix handle. Then KERNEL proceeds as follows:
- Error check KERNEL's input parameters.
- If the A_tunable has a tuned matrix representation, try to execute a matrix type-specific kernel.
- If there is no tuned representation or no type-specific kernel, try to execute a default kernel. For example, if the kernel is sparse
 , the default implementation executes multiplication by
, the default implementation executes multiplication by 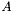 and by
and by  as separate sparse matrix-vector multiplies.
as separate sparse matrix-vector multiplies. - If the default kernel fails, check if A_tunable has a separate shared input matrix representation, and try to execute that representation's kernel (and default kernel if that fails).
- If no kernel could be execute successfully, call the error handler and return ERR_NOT_IMPLEMENTED.
- Otherwise, the kernel executed successfully. Record this kernel execution in the trace associated with A_tunable (see Tracing Module).
- Return 0 to indicate no errors occurred.
The library implementation distinguishes between these matrix type-independent kernels and matrix type-specific kernels. For sparse matrix-vector multiply, oski_MatMult(), defined in the public interface, is the type-independent kernel. Its corresponding type-dependent implementation is called oski_MatReprMult() and defined in the matrix type's module (see MATTYPES_INTERFACE).
|
Files |
| file | a_and_at.h |
| | Sparse simultaneous multiplication by 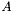 and and  . .
|
| file | ata.h |
| | Sparse  implementation. implementation.
|
| file | kerinfo.h |
| | Define the kernels available to the library.
|
| file | matmult.h |
| | Sparse matrix-vector multiply implementation.
|
| file | matpow.h |
| | Sparse  implementation. implementation.
|
| file | trisolve.h |
| | Sparse triangular solve implementation.
|
Generated on Wed Sep 19 16:41:23 2007 for BeBOP Optimized Sparse Kernel Interface Library by
 1.4.6
1.4.6
 .
. and
and  .
. .
. .
. and
and  .
. .
. , the default implementation executes multiplication by
, the default implementation executes multiplication by 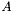 and by
and by  as separate sparse matrix-vector multiplies.
as separate sparse matrix-vector multiplies.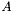 and
and  .
.  implementation.
implementation.  implementation.
implementation.  1.4.6
1.4.6