Block compressed sparse row (BCSR) format.
An 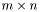 matrix
matrix 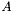 is stored in
is stored in 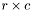 BCSR format using six arrays,
BCSR format using six arrays, 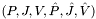 . The triplet
. The triplet 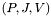 stores rows 1 through
stores rows 1 through 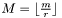 using uniformly aligned
using uniformly aligned 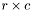 blocks, and the triplet
blocks, and the triplet 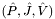 stores any remaining
stores any remaining 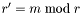 rows using uniformly aligned
rows using uniformly aligned 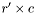 blocks.
blocks.
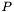 is an integer array of block-row pointers, of length at least
is an integer array of block-row pointers, of length at least 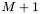 .
.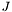 is an integer array of block column indices, of length at least
is an integer array of block column indices, of length at least ![$P[M]$](form_27.png) .
.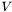 is an array of non-zero block values, of length at least
is an array of non-zero block values, of length at least ![$P[M]\cdot r\cdot c$](form_29.png) .
.
Define block-row 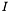 to be rows
to be rows 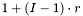 through
through 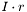 of
of 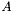 , where
, where 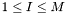 . For each
. For each 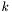 such that
such that ![$P[I-1] \leq k \leq P[I]$](form_35.png) ,
, ![$j_0=J[k]+1$](form_36.png) is the column index
is the column index 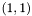 entry of an explicitly stored non-zero block whose values are laid out in row-major order in the subarray
entry of an explicitly stored non-zero block whose values are laid out in row-major order in the subarray ![$V[krc : (k+1)rc-1]$](form_38.png) .
.
These blocks are uniformly aligned, meaning that 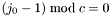 . However, there is one exception: if
. However, there is one exception: if 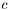 does not divide
does not divide 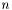 , then each block row may contain one block with
, then each block row may contain one block with 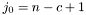 . If such a block overlaps with another block starting at column index
. If such a block overlaps with another block starting at column index 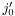 , then the initial columns of the block at
, then the initial columns of the block at 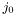 are set to zero.
are set to zero.
If 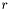 does not divide
does not divide 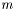 , then the remaining rows are stored in
, then the remaining rows are stored in 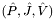 as a single block row with
as a single block row with 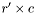 blocks. These arrays follow the same conventions as
blocks. These arrays follow the same conventions as 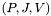 .
.
 1.4.6
1.4.6